Math 111: MATLAB Assignment 2: Newton's Method
Due Date: April 24, 2008
The sample program below illustrates how Newton's Method is used to find the root of an equation. Consult the MATLAB TA's if you have any questions.
Contents
Sample Program
Use Newton's method to find the one real root of
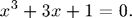
Note: anything following a '%' is a comment and is ignored by Matlab
x = -2; Tol = 0.0000001; count = 0; dx=1; %this is a fake value so that the while loop will execute f=-13; % because f(-2)=-13 fprintf('step x dx f(x)\n') fprintf('---- ----------- --------- ----------\n') fprintf('%3i %12.8f %12.8f %12.8f\n',count,x,dx,f) xVec=x;fVec=f; while (dx > Tol || abs(f)>Tol) %note that dx and f need to be defined for this statement to proceed count = count + 1; fprime = 3*x^2 + 3; xnew = x - (f/fprime); % compute the new value of x dx=abs(x-xnew); % compute how much x has changed since last step x = xnew; f = x^3 + 3*x + 1; % compute the new value of f(x) fprintf('%3i %12.8f %12.8f %12.8f\n',count,x,dx,f) end % This produces the following output:
step x dx f(x) ---- ----------- --------- ---------- 0 -2.00000000 1.00000000 -13.00000000 1 -1.13333333 0.86666667 -3.85570370 2 -0.57073065 0.56260268 -0.89809804 3 -0.34491904 0.22581161 -0.07579185 4 -0.32234116 0.02257788 -0.00051597 5 -0.32218536 0.00015580 -0.00000002 6 -0.32218535 0.00000001 0.00000000
New Matab ideas
- A While Loop. This begins with a line like 'while condition' and terminates with an 'end' statement. This while loop keeps running if either dx>Tol or f>Tol in absolute value (the '||' in the while statement means 'or'). It quits when both fall below the tolerance.
- the fprintf statement. This is a formatted printing statement, which uses almost identical syntax to the C programming language. It is used here to format the output for display. You should be able to use this part of the program without modifying it.
Description of parameters used in this program
x We start with an initial guess x = 0, x then gets updated by the newton iterations
N is the Maximum number of Iterations you will allow the program to do
Tol is the Tolerance, the max difference permitted between exact and approximate root
count is the number of iterations performed
Saving and ruunning the program
Once you have saved this program, for example as newton.m, typing the filename, newton, at the prompt in the Command window will run the program.
Your Assignment
Cut and paste the above code into the Matlab editor. Modify it appropriately to do the following to hand in:
1. Find the roots of the equation
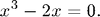
Use initial guesses of x=1. and x=-1. What happens if you give an initial guess of x=0? Explain.
2. Find the root of the equation

starting from the initial condition x=0.
How many iterations are required to obtain accuracy of 6 decimal places?
Hand in printouts of both the m-files and the outputs of the two programs.